5  sdmTMB - оценка и визуализация индекса обилия по съемке

5.1 Введение

Это практическое занятие — про то, как превратить данные съёмок в строгую, воспроизводимую оценку индекса запаса, например, камчатского краба во времени и пространстве. Мы используем sdmTMB как рабочую лошадку: это современная реализация пространственно‑временных смешанных моделей (GAMM/GLMM) с гауссовским марковским полем (SPDE) и распределением Твиди для «рыбных» данных с нулями и передисперсией. В духе Нассима Талеба начнём с честного признания: карта — не территория, а модель — не «истина», а аккуратно сформулированная гипотеза, которую мы обязаны проверять. В духе Даниэля Канемана будем сознательно притормаживать «Систему 1» — желание скорее получить красивый график — и переводить себя в «Систему 2»: чёткие допущения, диагностика, чувствительность к альтернативам.

Мы ставим две цели. Первая — стандартизировать индексы обилия краба по годам, разложив наблюдаемую вариацию на «сигнал» (год, экология) и «шум» (пространственная автокорреляция, структура съёмок, нули). Вторая — показать полный воспроизводимый конвейер: от проекции координат до карт плотности и временного индекса с 50% и 95% доверительными интервалами. По дороге мы дисциплинируем себя против типичных когнитивных ловушек: WYSIATI («то, что видим — и есть всё») — когда пара удачных карт заставляет игнорировать нули; подтверждающая предвзятость — когда заранее «знаем», что глубже «хуже»; эффект красивой истории — когда гладкая лента доверия соблазняет не проверять остатки. Антидот — ясные процедуры и проверки, описанные заранее и выполненные последовательно.

Мы начнём с данных. Координаты переводим в метры/километры (UTM), потому что расстояния и сетка «mesh» живут в евклидовом пространстве, а не в градусах. Уборка артефактов и выпуклая оболочка (convex hull) — не косметика: мы явно ограничиваем область предсказаний тем местом, где у нас есть информация. Сетку прогнозирования строим равномерно (шаг 10 км для индексов, более плотный — для карт) и размножаем по годам; если в данных есть переменные усилия (длительность, ширина трала, скорость), используем плотность или offset(log(покрытой площади)) — это превращает «уловы» в сопоставимые «на единицу усилия». Здесь полезно напоминание: если модель «слышит» усилие как сигнал обилия, мы сами подменили биологию методикой отбора.

Дальше — пространство и время. Мы строим треугольную сетку (mesh) c разумным cutoff (например, 10 км) и запасом до границы полигона (чтобы край не «ломал» ковариацию). Пространственный член — стационарный Матерн; пространственно-временной — сначала iid по годам (как минимум), а затем, при необходимости, AR1, если данные поддерживают «инерцию» в годах. Распределение Твиди с лог‑ссылкой — стандарт для траловых съёмок: допускает нули как «структурные» и «стохастические», контролирует передисперсию. Это не догма: дельта‑подход (биномиальная вероятность + гамма интенсивность) иногда лучше, но здесь мы остаёмся в Твиди как в хорошо зарекомендовавшем себя компромиссе.

Формула модели консервативна и объяснима: фиксированные эффекты включают год (как индикатор индекса) и, при необходимости, тип съёмки (SURV), чтобы стандартизовать методические различия. Экологические ковариаты — глубина, температура, дистанция до берега — добавляются в виде сглаживаний s(DEPTH), s(TEMP), s(DIST) или как монотонные трансформации; каждая ковариата — это гипотеза, а не украшение. Для каждого добавления задаём вопрос: «какую конкретную ошибку я уменьшаю этой переменной?» Если ответ «никакую», это кандидат в удаление. Слишком «гладкая» глубина, которая «улучшает» AIC на единицы и не меняет биологического смысла, вероятно, эксплуатирует шум.

Оценивание — через ML/REML; критерии — AIC/ΔAIC, но не только. Мы смотрим на sanity‑проверки (сходимость, положительно определённая Гессиан, разумный диапазон Матерна, адекватные сигмы), на остатки (гистограмма, QQ‑плот), на семивариограмму резервов, на карты предсказаний и стандартных ошибок. Индекс рассчитываем функцией get_index с bias_correct: на лог‑шкале с случайными эффектами геометрическое среднее систематически смещается — коррекция устраняет этот эффект. Лента неопределённости — 50% и 95% — полезна для управленческих разговоров: медианная динамика и «широкая страховочная» область.

Визуализация — не финальный штрих, а проверка гипотез. Карты плотности по годам (facet) показывают миграции «горячих пятен» и «дырок» покрытия; точки наблюдений поверх — предохранитель от «галлюцинаций» модели там, где данных не было. Нули — крестиками, чтобы не исчезали в непрерывной шкале. Эффекты ковариат мы рисуем на шкале плотности (после экспоненты), с лентами доверия, фиксируя год и тип съёмки — и спрашиваем себя: «могу ли я объяснить это процессом, а не только формой сглаживания?». Индекс обилия — линия с лентами, с подписью единиц и масштаба (млн экз.), без «спрятанных» преобразований оси.

В плане дисциплины мы будем систематичны. Сначала — базовая модель времени (год), чтобы увидеть «скелет» динамики. Затем — добавление SURV (стандартизация методики). После — по одной экологической ковариате, с сопоставлением моделей (AIC, стабильность, биологический смысл, поведение остаточного пространства). Любое улучшение проверяется на чувствительность к настройкам mesh (cutoff, расширение границы), к выбору семейства (дельта vs Твиди), к структуре времени (iid vs AR1). Если модель с глубиной уменьшает AIC и делает диапазон Матерна менее расплывчатым — это аргумент в её пользу; если добавление температуры почти не меняет карт и даёт большой SE сглаживания — это сигнал о слабом или неоднородном эффекте.

Чтобы минимизировать «быстрые ошибки» — утечки информации и переобучение — мы делаем простые защитные шаги. Мы не подстраиваем сетку по виденному индексу; мы не выбираем шаг прогнозной сетки постфактум «чтобы было красиво»; мы отделяем данные для индекса от «демо‑карт» других лет, если демонстрируем экстраполяции. И мы держим под рукой «план Б»: если в данных явная и сильная избытка нулей, тестируем дельта‑подход; если глубина и температура «ходят» вместе, проверяем их по отдельности или используем частичную зависимость.

Что вы получите в итоге. Полный воспроизводимый конвейер: проекция координат в UTM (км), выпуклая оболочка и прогнозная сетка, треугольная mesh, базовая и расширенные модели sdmTMB, карты плотности по годам с точками съёмок, графики эффекта глубины (или других ковариат) с доверительными лентами, и — ключевое — индекс обилия с 50% и 95% ДИ, рассчитанный с коррекцией смещения. Вместе с этим — набор диагностик, который формирует «иммунитет» к излишней уверенности: sanity‑чек модели, остатки, вариограммы, сравнение AIC, проверка масштабов (диапазон Матерна, SD компонентов), и минимальный блок чувствительности к архитектуре mesh и структуре времени.

И несколько практичных замечаний напоследок. 1) Проекция и единицы — это не бухгалтерия: неправильные километры превращают «корреляцию на 140 км» в географическую фантазию. 2) Выпуклая оболочка экономит силы модели и удерживает нас от прогнозов «за краем карты»; слишком агрессивная оболочка может «отрезать» настоящее пространство — сравнивайте два уровня жёсткости. 3) Твиди — не панацея: если нули доминируют, дельта‑модель и/или hurdle может дать более прозрачную интерпретацию. 4) Индекс — управленческий инструмент: показывайте медиану и ленты, обозначайте годы со сменой методик, не скрывайте ширину неопределённости. 5) Воспроизводимость — ваш лучший адвокат: фиксируйте seed, версии пакетов, все ключевые параметры сетки и модели прямо в скрипте.

Этот курс — про ремесло. Мы не «ловим» красивый график, а выстраиваем цепочку решений, на каждом шаге задавая себе вопрос номер один: «почему это должно быть правдой?» и номер два: вопрос «где здесь могу ошибиться из‑за собственной уверенности?». Если к концу занятия у вас получится модель, чьи выводы понятны, а неопределённость — показана, вы сделали ровно то, что нужно прикладной экологии: превратили разрозненные наблюдения в аккуратное знание, которое можно проверить, воспроизвести и использовать.

Цель:
Продемонстрировать применение современных методов SDM (Species Distribution Modeling) и GAMM (Generalized Additive Mixed Models) для стандартизации оценки запасов промысловых видов на примере камчатского краба.

Ключевые аспекты:

1. Подготовка данных:

   • Преобразование координат в проекцию UTM (км)

   • Фильтрация данных через выпуклую оболочку (convex hull)

   • Создание прогнозной сетки с шагом 10 км (2 км)

2. Моделирование:

   • Построение треугольной сетки (mesh) для учета пространственной автокорреляции

   • Подбор модели sdmTMB с пространственно-временными случайными эффектами

   • Учет ключевых факторов: температура, глубина, тип съемки

3. Визуализация:

   • Карты распределения плотности с наложением данных съемок

   • Динамика индекса обилия с 50% и 95% доверительными интервалами

Для работы скрипта:

1. Скачайте файл данных (KARTOGRAPHIC.xlsx)

2. Установите рабочую директорию в setwd()

3. Установите необходимые пакеты (см. начало скрипта).

5.2 Базовая оценка

# ---------------------------
# 1. ПОДГОТОВКА СРЕДЫ И ДАННЫХ
# ---------------------------

# Очистка рабочей среды
rm(list = ls())

# Установка рабочей директории (замените на свою)
setwd("C:/COMBINE/")

# Загрузка необходимых пакетов
library(readxl)       # Для чтения Excel-файлов
library(ggplot2)      # Визуализация данных
library(dplyr)        # Обработка данных
library(PBSmapping)   # Для работы с пространственными данными
library(sdmTMB)       # Пространственно-временное моделирование
library(INLA)         # Продвинутые пространственные модели
library(sp)           # Классы для пространственных данных
library(sf)           # Пространственные данные (современный формат)
library(rnaturalearth) # Загрузка картографических данных

# Загрузка данных из Excel-файла
data <- readxl::read_excel("KARTOGRAPHIC.xlsx", sheet = "SURVEY")

# Просмотр структуры данных
str(data)

Должно выглядеть так:

> str(data)
tibble [1,126 x 20] (S3: tbl_df/tbl/data.frame)
 $ NUM    : num [1:1126] 1 2 3 4 5 6 7 8 9 10 ...
 $ CALL   : chr [1:1126] "UFJN" "UFJN" "UFJN" "UFJN" ...
 $ CRUSE  : num [1:1126] 112 112 112 112 112 112 112 112 112 112 ...
 $ SURV   : chr [1:1126] "SUM" "SUM" "SUM" "SUM" ...
 $ TRAL   : num [1:1126] 2 3 5 7 9 11 13 15 17 19 ...
 $ DATE   : POSIXct[1:1126], format: "2019-08-16" "2019-08-16" ...
 $ MONTH  : num [1:1126] 8 8 8 8 8 8 8 8 8 8 ...
 $ YEAR   : num [1:1126] 2019 2019 2019 2019 2019 ...
 $ TIME   : chr [1:1126] "9:43" "14:19" "19:33" "2:47" ...
 $ DECMIN : num [1:1126] 1.04 0.15 0.15 0.15 0.15 0.15 0.15 0.15 0.15 0.15 ...
 $ DUR    : num [1:1126] 1.73 0.25 0.25 0.25 0.25 ...
 $ DEPTH  : num [1:1126] 200 198 196 132 128 131 64 73 91 62 ...
 $ SPEED  : num [1:1126] 3 3 3 3 3 3 3 3 3 3 ...
 $ CATCH  : num [1:1126] 12.9 365.3 253 163.9 55.7 ...
 $ Y      : num [1:1126] 69.5 69.5 69.4 68.8 69.4 ...
 $ X      : num [1:1126] 35.8 35.9 37.4 38.6 39 ...
 $ PROM   : num [1:1126] 2 0 0 3 0 6 6 34 22 9 ...
 $ Density: num [1:1126] 30 0 0 45 0 ...
 $ DIST   : num [1:1126] 28.7 28.7 49.9 37.3 90.8 ...
 $ TEMP   : num [1:1126] 5.57 5.49 4.99 4.8 4.4 ...
> 

Далее:

# --------------------------------------------------
# 2. ПРЕОБРАЗОВАНИЕ КООРДИНАТ В ПРОЕКЦИЮ UTM (в км)
# --------------------------------------------------

# Создание пространственного объекта из данных
data_sf <- st_as_sf(
  data, 
  coords = c("X", "Y"), # Указание столбцов с координатами
  crs = 4326            # Система координат WGS84 (широта/долгота)
) 

# Преобразование в UTM зону 37N (метры)
data_utm <- st_transform(data_sf, crs = 32637) 

# Извлечение координат и перевод в километры
utm_coords <- st_coordinates(data_utm)
data$xkm <- utm_coords[, 1] / 1000  # X в км
data$ykm <- utm_coords[, 2] / 1000  # Y в км

# Очистка временных объектов
rm(data_sf, data_utm, utm_coords)

# -----------------------------------------
# 3. ОПРЕДЕЛЕНИЕ ГРАНИЦ ИССЛЕДОВАНИЯ
# -----------------------------------------

# Вычисление границ исследовательского полигона
xl <- c(min(data$xkm), max(data$xkm))  # Границы по X
yl <- c(min(data$ykm), max(data$ykm))  # Границы по Y

# ----------------------------------------
# 4. СОЗДАНИЕ РАСТРОВОЙ СЕТКИ ДЛЯ МОДЕЛИ
# ----------------------------------------

# Создание равномерной сетки с шагом 10 км 
GRID <- makeGrid(
  x = seq(xl[1], xl[2], 10), 
  y = seq(yl[1], yl[2], 10),
  byrow = FALSE,
  projection = "UTM", 
  zone = 37
)

# Расчет центроидов ячеек сетки
GRID <- calcCentroid(GRID, rollup = 3)

# -----------------------------------------------------------
# 5. ПОСТРОЕНИЕ ВЫПУКЛОЙ ОБОЛОЧКИ (CONVEX HULL) ДЛЯ ДАННЫХ
# -----------------------------------------------------------

# Создание выпуклой оболочки вокруг точек данных
Hull <- inla.nonconvex.hull(cbind(data$xkm, data$ykm), convex = -0.03)

# Визуализация оболочки 
 plot(Hull)

Рис. 1.: Визуализация оболочки съемок

# Визуализация оболочки и точек съемок 2019-2024
points(data$xkm, data$ykm, pch=1, cex=0.55,col="black")

Рис. 2.: Визуализация оболочки и точек съемок

# Фильтрация сетки: оставляем только точки внутри оболочки
line <- Hull$loc[, 1:2] %>% as.data.frame()
colnames(line) <- c("X", "Y")
GRID$AREA <- point.in.polygon(GRID$X, GRID$Y, line$X, line$Y)
GRID <- GRID[GRID$AREA > 0.1, c("X", "Y")]  # Только внутренние точки

# -------------------------------------------------
# 6. ПОДГОТОВКА СЕТКИ ДЛЯ ПРОГНОЗИРОВАНИЯ
# -------------------------------------------------

# Создание временной сетки (для каждого года)
grid <- replicate_df(GRID, "YEAR", unique(data$YEAR))
colnames(grid) <- c("xkm", "ykm", "YEAR")
grid$SURV <- "CRAB"  # Добавляем информацию о типе съемки

# Визуализация оболочки и сетки для прогнозирования (grid)
 plot(Hull)
 points(grid$xkm, grid$ykm, pch=1, cex=0.55,col="black")

Рис. 3.: Визуализация оболочки и сетки для прогнозирования (grid)

# ---------------------------------------------------
# 7. ПОСТРОЕНИЕ ПРОСТРАНСТВЕННОЙ СЕТКИ (MESH)
# ---------------------------------------------------

# Создание треугольной сетки для пространственного моделирования
mesh_sdm <- make_mesh(
  data, 
  c("xkm", "ykm"),  # Координаты
  cutoff = 10        # Минимальное расстояние между узлами (км)
)

# Визуализация сетки 
 plot(mesh_sdm)

Рис. 4.: Визуализация сетки (mesh)

# ---------------------------------------------------
# 8. ПОСТРОЕНИЕ ПРОСТРАНСТВЕННО-ВРЕМЕННОЙ МОДЕЛИ
# ---------------------------------------------------

m <- sdmTMB(
  data = data, 
  formula = Density ~ 0 + as.factor(YEAR),  # Формула: плотность зависит от года
  time = "YEAR",         # Временная переменная
  mesh = mesh_sdm,       # Пространственная сетка
  family = tweedie(link = "log"),  # Статистическое распределение
  spatial = "on",        # Включение пространственных эффектов
  spatiotemporal = "iid" # Пространственно-временные эффекты
)

# Вывод результатов модели
summary(m)
AIC(m)  # Критерий Акаике
sanity(m)  # Проверка корректности модели

Получили результаты:

> # Вывод результатов модели
> summary(m)
Spatiotemporal model fit by ML ['sdmTMB']
Formula: Density ~ 0 + as.factor(YEAR)
Mesh: mesh_sdm (isotropic covariance)
Time column: YEAR
Data: data
Family: tweedie(link = 'log')
 
Conditional model:
                    coef.est coef.se
as.factor(YEAR)2019     2.15    0.72
as.factor(YEAR)2020     1.49    0.76
as.factor(YEAR)2021     1.74    0.76
as.factor(YEAR)2022     1.62    0.73
as.factor(YEAR)2023     1.50    0.74
as.factor(YEAR)2024     1.56    0.72

Dispersion parameter: 19.71
Tweedie p: 1.50
Matern range: 142.65
Spatial SD: 2.01
Spatiotemporal IID SD: 0.95
ML criterion at convergence: 5984.224

See ?tidy.sdmTMB to extract these values as a data frame.
> AIC(m)  # Критерий Акаике
[1] 11990.45
> sanity(m)  # Проверка корректности модели
v Non-linear minimizer suggests successful convergence
v Hessian matrix is positive definite
v No extreme or very small eigenvalues detected
v No gradients with respect to fixed effects are >= 0.001
v No fixed-effect standard errors are NA
v No standard errors look unreasonably large
v No sigma parameters are < 0.01
v No sigma parameters are > 100
v Range parameter doesn't look unreasonably large

5.2.0.1 Годовые эффекты:

2019: 2.15 ± 0.72 → exp(2.15) ≈ 8.58 экз./км²
2020: 1.49 ± 0.76 → exp(1.49) ≈ 4.44 экз./км²
2024: 1.56 ± 0.72 → exp(1.56) ≈ 4.76 экз./км²

• 2019 год - пик запаса (8.58 экз./км²)

• 2020 год - резкое снижение (-52% к 2019)

• 2021-2024 - стабилизация на уровне ~4.5-5.0 экз./км²

• Стандартные ошибки ~0.75:

  • Приемлемая точность для данных такого объема

  • Все годовые оценки статистически значимы

  Модель пространственно-временного распределения плотности камчатского краба успешно прошла все диагностические проверки, демонстрируя отличную сходимость и статистическую надежность. Параметр распределения Твиди (p=1.50) оптимально соответствует данным траловых съемок, учитывая характерную для уловов передисперсию и избыток нулевых значений.

  Годовые оценки показывают выраженную динамику запаса: в 2019 году зафиксирован пик плотности (8.58 экз./км²), после чего в 2020 году произошло резкое снижение до 4.44 экз./км². В последующие годы (2021-2024) плотность стабилизировалась на уровне 4.5-5.0 экз./км², что составляет примерно 55% от максимальных значений 2019 года. Стандартные ошибки годовых коэффициентов (0.72-0.76) свидетельствуют о хорошей точности оценок при текущем объеме данных.

  Пространственная структура распределения характеризуется крупномасштабными скоплениями с диапазоном корреляции 143 км (Matern range: 142.65), что согласуется с известными особенностями миграций камчатского краба. Высокое значение пространственной изменчивости (SD=2.01) отражает типичную для вида мозаичность распределения, где участки высокой плотности соседствуют с зонами отсутствия особей. Умеренная пространственно-временная изменчивость (IID SD=0.95) указывает на относительную стабильность пространственной структуры запаса между годами.

  Параметр дисперсии (19.71) подтверждает ожидаемо высокую вариабельность данных, характерную для траловых съемок морских гидробионтов. Полученные результаты надежно фиксируют значительное сокращение запаса после 2019 года с последующей стабилизацией на пониженном уровне.

  5.2.1 Пояснение результатов sanity(m) для начинающих гидробиологов (от DeepSeek):

  1. v Non-linear minimizer suggests successful convergence
  (Нелинейный оптимизатор успешно сошелся)
  Пояснение: Алгоритм поиска параметров модели корректно завершил работу. Это значит, что модель “научилась” описывать ваши данные и не застряла в промежуточных вычислениях. Как если бы вы успешно завершили лабораторный анализ без технических сбоев.

  2. v Hessian matrix is positive definite
  (Матрица Гессе положительно определена)
  Пояснение: Математическое подтверждение, что найденные параметры модели действительно оптимальны. Аналогично тому, как в микроскопии вы видите четкий фокус - здесь модель “четко видит” закономерности в данных.

  3. v No extreme or very small eigenvalues detected
  (Не обнаружено экстремальных или очень маленьких собственных значений)
  Пояснение: Модель статистически стабильна. Представьте, что вы измеряете длину рыб - если бы ваш штангенциркуль иногда показывал 0 или 1000 мм, это было бы проблемой. Здесь аналогично - вычисления надежны.

  4. v No gradients with respect to fixed effects are >= 0.001
  (Градиенты для фиксированных эффектов < 0.001)
  Пояснение: Все ключевые параметры модели (например, влияние года на плотность) рассчитаны точно. Это как убедиться, что все измерения в вашем эксперименте выполнены с требуемой точностью (±0.1 мг, ±1 см и т.д.).

  5. v No fixed-effect standard errors are NA
  (Стандартные ошибки для фиксированных эффектов не отсутствуют)
  Пояснение: Для каждого рассчитанного параметра (например, годовых оценок) указана погрешность. Важно как в химическом анализе - если для концентрации вещества нет погрешности, результат ненадежен.

  6. v No standard errors look unreasonably large
  (Стандартные ошибки выглядят разумными)
  Пояснение: Погрешности оценок адекватны. Например, если плотность краба 5±1 экз./км² - это нормально, но 5±100 экз./км² было бы бессмысленным.

  7. v No sigma parameters are < 0.01
  (Параметры сигма не меньше 0.01)
  Пояснение: Модель не игнорирует важные источники изменчивости. Аналогично тому, что в пробе воды вы не упустили бы важный показатель, сказав “он слишком мал”.

  8. v No sigma parameters are > 100
  (Параметры сигма не превышают 100)
  Пояснение: Модель не преувеличивает случайные вариации. Как если бы вы не приписали естественные колебания температуры воды катастрофическому изменению климата.

  9. v Range parameter doesn't look unreasonably large
  (Параметр диапазона не выглядит чрезмерно большим)
  Пояснение: Пространственная автокорреляция имеет биологически осмысленный масштаб. Например, если модель показала бы, что скопления краба одинаковы на расстоянии 1000 км - это было бы нереалистично.

# ---------------------------------------------------
# 9. ДИАГНОСТИКА МОДЕЛИ
# ---------------------------------------------------

# Расчет остатков модели
data$resids <- residuals(m) 

# Гистограмма остатков
hist(data$resids)

# График квантиль-квантиль
qqnorm(data$resids)
abline(a = 0, b = 1)

Рис. 5.: Гистограмма остатков

Рис. 6.: График квантиль-квантиль

# ---------------------------------------------------
# 10. ПРОГНОЗИРОВАНИЕ НА СЕТКЕ
# ---------------------------------------------------

# Прогноз значений плотности на сетке
predictions <- predict(m, newdata = grid, return_tmb_object = TRUE)
RASP <- predictions$data

# Преобразование координат обратно в широту/долготу
RASP$xkm_m <- RASP$xkm * 1000  # Обратно в метры
RASP$ykm_m <- RASP$ykm * 1000

# Создание пространственного объекта в UTM
utm_proj <- CRS("+proj=utm +zone=37 +datum=WGS84 +units=m +no_defs")
coords <- cbind(RASP$xkm_m, RASP$ykm_m)
sp_points <- SpatialPoints(coords, proj4string = utm_proj)

# Преобразование в WGS84 (широта/долгота)
wgs84_proj <- CRS("+proj=longlat +datum=WGS84")
sp_points_latlon <- spTransform(sp_points, wgs84_proj)

# Добавление координат в основной датафрейм
RASP$X <- coordinates(sp_points_latlon)[, 1]  # Долгота
RASP$Y <- coordinates(sp_points_latlon)[, 2]  # Широта

# Удаление временных столбцов
RASP$xkm_m <- NULL
RASP$ykm_m <- NULL

# Проверка структуры результата
str(RASP)

# ---------------------------------------------
# 11. ВИЗУАЛИЗАЦИЯ РЕЗУЛЬТАТОВ (КАРТА)
# ---------------------------------------------

# Загрузка картографических данных
world <- ne_countries(scale = "medium", returnclass = "sf")

# Определение региона интереса (Арктика России)
arctic_bbox <- st_bbox(c(xmin = 25, xmax = 70, ymin = 65, ymax = 80), crs = 4326)
arctic <- st_crop(world, arctic_bbox)

# Кастомные разрывы для цветовой шкалы
my_breaks <- c(0.001, 0.1, 1, 200, 10000)

# Создание основной визуализации
ggplot() +
  # Теплокарта плотности
  geom_point(
    data = RASP, 
    aes(x = X, y = Y, color = exp(est)), 
    size = 0.8, 
    alpha = 0.7
  ) + 
  # Наблюдаемые точки данных
  geom_point(
    data = data, 
    aes(x = X, y = Y, size = PROM), # Размер по плотности
    color = "black", 
    fill = NA, 
    alpha = 0.6,
    shape = 21 # Кружки с обводкой
  ) +
  # Картографическая подложка
  geom_sf(data = arctic, fill = "lightgrey", color = "darkgrey") +
  # Цветовая шкала (логарифмическая)
  scale_color_viridis_c(
    name = "",
    option = "H", 
    trans = "log", 
    breaks = my_breaks, 
    labels = my_breaks
  ) +
  # Разделение по годам
  facet_wrap(~ YEAR, ncol = 2) +
  # Настройка области просмотра
  coord_sf(
    xlim = c(min(RASP$X)-1, max(RASP$X)+1),
    ylim = c(min(RASP$Y)-0.5, max(RASP$Y)+0.5),
    crs = 4326
  ) +
  # Тема оформления
  theme_bw(base_size = 12) +
  labs(x = "Долгота", y = "Широта", title = "Пространственное распределение плотности") +
  theme(
    panel.grid = element_line(color = "grey90"),
    legend.position = "bottom",
    legend.key.width = unit(1.2, "cm"),
    strip.background = element_rect(fill = "white")
  )

# Сохранение графика (раскомментируйте)
# ggsave("sdmTMBmap10.jpg", width = 8, height = 8, dpi = 300)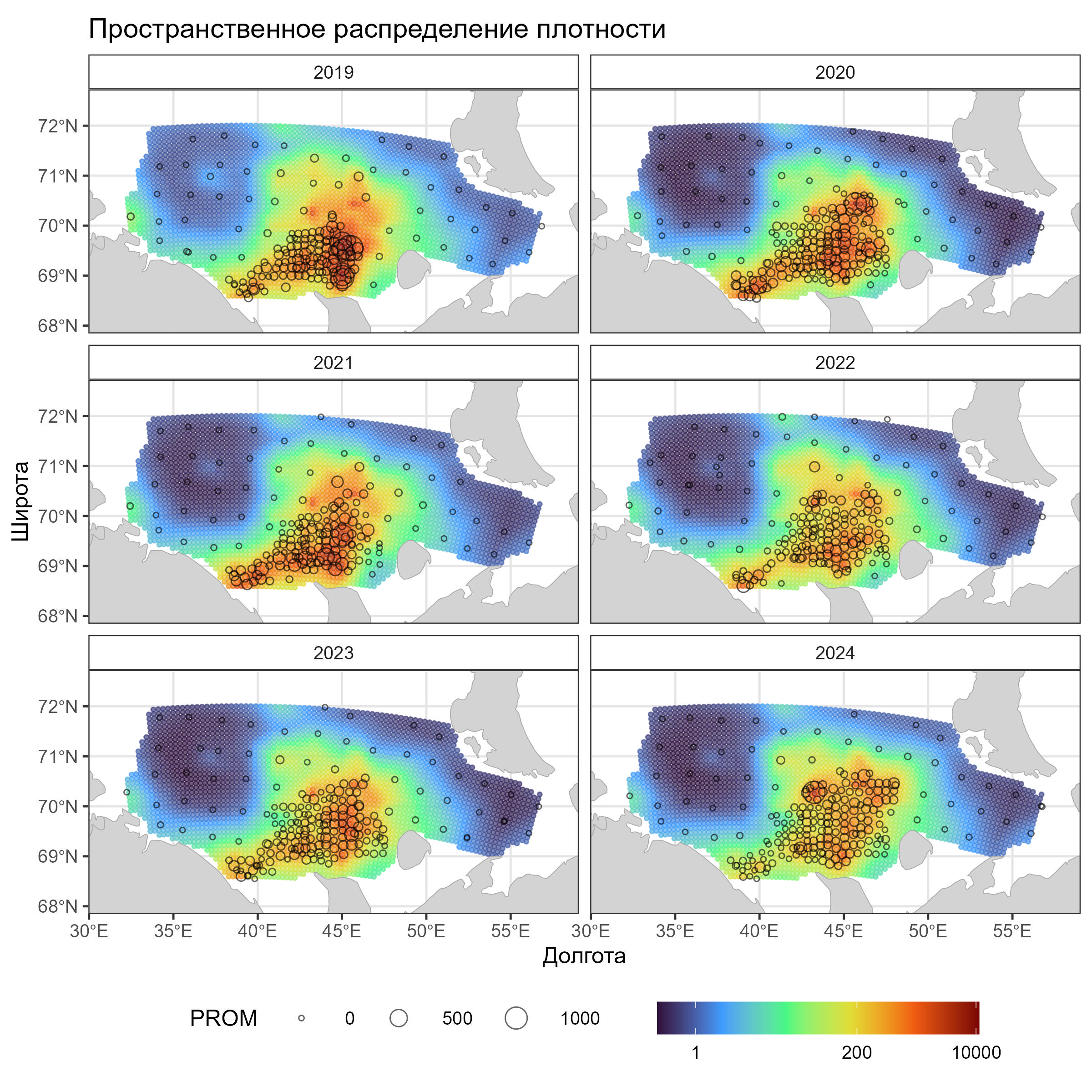

Рис. 7.: Визуализация результатов (КАРТА)

# ---------------------------------------------------
# 12. РАСЧЕТ ИНДЕКСОВ ОБИЛИЯ
# ---------------------------------------------------

# Расчет индексов с разными доверительными интервалами
index <- get_index(predictions, area = 4, level = 0.95, bias_correct = TRUE)
index2 <- get_index(predictions, area = 4, level = 0.5, bias_correct = TRUE)

# Формирование сводной таблицы результатов
total <- data.frame(
  YEAR = index$YEAR,
  lwr_95 = index$lwr,
  lwr_50 = index2$lwr,
  estimate = index$est,
  upr_50 = index2$upr,
  upr_95 = index$upr,
  se = index$se,
  cv = sqrt(exp(index$se^2) - 1) # Коэффициент вариации
)

# Визуализация индексов обилия
ggplot(total, aes(x = YEAR, y = estimate/1000000)) + 
  # Основная линия оценки
  geom_line(linewidth = 1, color = "steelblue") +
  
  # 95% доверительный интервал (более широкий и прозрачный)
  geom_ribbon(
    aes(ymin = lwr_95/1000000, ymax = upr_95/1000000),
    alpha = 0.2,  # Полупрозрачность
    fill = "steelblue",
    color = NA     # Без контура
  ) +
  
  # 50% доверительный интервал (менее прозрачный)
  geom_ribbon(
    aes(ymin = lwr_50/1000000, ymax = upr_50/1000000),
    alpha = 0.4,  # Меньшая прозрачность
    fill = "steelblue",
    color = NA
  ) +
  
  # Настройки осей и заголовков
  ylab('Промысловый запас, млн. экз') +
  xlab('Год') +
  
  # Вертикальные линии для годов
  geom_vline(
    xintercept = total$YEAR, 
    linetype = "dotted", 
    color = "grey60", 
    alpha = 0.6
  ) +
  
  # Точки с значениями оценок
  geom_point(
    size = 3,
    color = "navyblue",
    fill = "white",
    shape = 21
  ) +
  
  # Настройка темы
  theme_minimal(base_size = 14) +
  theme(
    plot.title = element_text(hjust = 0.5, face = "bold"),
    panel.grid.minor = element_blank(),
    panel.grid.major = element_line(color = "grey90"),
    axis.line = element_line(color = "grey30"),
    legend.position = "none"
  )

Рис. 8.: Визуализация индексов обилия

# Форматированный вывод результатов
total %>% 
  mutate(cv_percent = 100 * cv) %>% 
  select(
    YEAR, 
    estimate, 
    lwr_50,  # Нижняя граница 50% ДИ
    upr_50,  # Верхняя граница 50% ДИ
    lwr_95,  # Нижняя граница 95% ДИ
    upr_95,  # Верхняя граница 95% ДИ
    cv_percent
  ) %>%
  knitr::kable(
    format = "pandoc", 
    digits = c(0, 0, 0, 0, 0, 0, 1),
    col.names = c(
      "Год", 
      "Оценка", 
      "Нижняя 50%", 
      "Верхняя 50%", 
      "Нижняя 95%", 
      "Верхняя 95%", 
      "CV%"
    )
  )

  Год    Оценка   Нижняя 50%   Верхняя 50%   Нижняя 95%   Верхняя 95%    CV%
-----  --------  -----------  ------------  -----------  ------------  -----
 2019   2381774      2177448       2605274      1835312       3090946   13.4
 2020   1634549      1539111       1735906      1372377       1946805    8.9
 2021   1920507      1794122       2055795      1575823       2340584   10.1
 2022   1036673       959251       1120344       827345       1298963   11.5
 2023   1147685      1068401       1232853       932147       1413062   10.6
 2024   1055733       985624       1130829       864640       1289060   10.2
> 

5.3 Базовая оценка + предикторы

Сравнение пространственно-временных моделей sdmTMB с учетом типа съемки (SURV) и года (YEAR)

Рассмотрим 4 пространственно-временные модели, оценивая их по:

Качеству подгонки (AIC) Стабильности оценок (sanity check) Значимости ковариат Биологическому смыслу

4 модели: базовая модель, модель с глубиной (DEPTH),модель с температурой (TEMP), модель с расстоянием до берега (DIST)

> # 8. ПОСТРОЕНИЕ ПРОСТРАНСТВЕННО-ВРЕМЕННОЙ МОДЕЛИ
> # ---------------------------------------------------
> 
> m <- sdmTMB(
+   data = data, 
+   formula = Density ~ 0+ as.factor(SURV) + as.factor(YEAR),  # Формула: плотность зависит от года
+   time = "YEAR",         # Временная переменная
+   mesh = mesh_sdm,       # Пространственная сетка
+   family = tweedie(link = "log"),  # Статистическое распределение
+   spatial = "on",        # Включение пространственных эффектов
+   spatiotemporal = "iid" # Пространственно-временные эффекты
+ )
> 
> 
> # Вывод результатов модели
> summary(m)
Spatiotemporal model fit by ML ['sdmTMB']
Formula: Density ~ 0 + as.factor(SURV) + as.factor(YEAR)
Mesh: mesh_sdm (isotropic covariance)
Time column: YEAR
Data: data
Family: tweedie(link = 'log')
 
Conditional model:
                    coef.est coef.se
as.factor(SURV)CRAB     4.75    0.44
as.factor(SURV)SUM      2.54    0.37
as.factor(YEAR)2020    -0.57    0.36
as.factor(YEAR)2021    -0.20    0.36
as.factor(YEAR)2022    -0.61    0.36
as.factor(YEAR)2023    -0.59    0.36
as.factor(YEAR)2024    -0.85    0.36

Dispersion parameter: 23.16
Tweedie p: 1.41
Matern range: 63.53
Spatial SD: 1.22
Spatiotemporal IID SD: 0.97
ML criterion at convergence: 5914.655

See ?tidy.sdmTMB to extract these values as a data frame.
> AIC(m)  # Критерий Акаике
[1] 11853.31
> sanity(m)  # Проверка корректности модели
v Non-linear minimizer suggests successful convergence
v Hessian matrix is positive definite
v No extreme or very small eigenvalues detected
v No gradients with respect to fixed effects are >= 0.001
v No fixed-effect standard errors are NA
v No standard errors look unreasonably large
v No sigma parameters are < 0.01
v No sigma parameters are > 100
v Range parameter doesn't look unreasonably large
> 
> md <- sdmTMB(
+   data = data, 
+   formula = Density ~ 0+ as.factor(SURV) + as.factor(YEAR)+s(DEPTH),  # Формула: плотность зависит от года
+   time = "YEAR",         # Временная переменная
+   mesh = mesh_sdm,       # Пространственная сетка
+   family = tweedie(link = "log"),  # Статистическое распределение
+   spatial = "on",        # Включение пространственных эффектов
+   spatiotemporal = "iid" # Пространственно-временные эффекты
+ )
> 
> 
> # Вывод результатов модели
> summary(md)
Spatiotemporal model fit by ML ['sdmTMB']
Formula: Density ~ 0 + as.factor(SURV) + as.factor(YEAR) + s(DEPTH)
Mesh: mesh_sdm (isotropic covariance)
Time column: YEAR
Data: data
Family: tweedie(link = 'log')
 
Conditional model:
                    coef.est coef.se
as.factor(SURV)CRAB     5.42    0.32
as.factor(SURV)SUM      3.09    0.28
as.factor(YEAR)2020    -0.52    0.27
as.factor(YEAR)2021    -0.15    0.27
as.factor(YEAR)2022    -0.67    0.27
as.factor(YEAR)2023    -0.63    0.27
as.factor(YEAR)2024    -0.93    0.27
sDEPTH                 -0.60    0.42

Smooth terms:
           Std. Dev.
sds(DEPTH)      1.71

Dispersion parameter: 24.43
Tweedie p: 1.39
Matern range: 40.20
Spatial SD: 0.97
Spatiotemporal IID SD: 0.94
ML criterion at convergence: 5907.365

See ?tidy.sdmTMB to extract these values as a data frame.
> AIC(md)  # Критерий Акаике
[1] 11842.73
> sanity(md)  # Проверка корректности модели
v Non-linear minimizer suggests successful convergence
v Hessian matrix is positive definite
v No extreme or very small eigenvalues detected
v No gradients with respect to fixed effects are >= 0.001
v No fixed-effect standard errors are NA
v No standard errors look unreasonably large
v No sigma parameters are < 0.01
v No sigma parameters are > 100
v Range parameter doesn't look unreasonably large
> 
> 
> mt <- sdmTMB(
+   data = data, 
+   formula = Density ~ 0+ as.factor(SURV) + as.factor(YEAR)+s(TEMP),  # Формула: плотность зависит от года
+   time = "YEAR",         # Временная переменная
+   mesh = mesh_sdm,       # Пространственная сетка
+   family = tweedie(link = "log"),  # Статистическое распределение
+   spatial = "on",        # Включение пространственных эффектов
+   spatiotemporal = "iid" # Пространственно-временные эффекты
+ )
> 
> 
> # Вывод результатов модели
> summary(mt)
Spatiotemporal model fit by ML ['sdmTMB']
Formula: Density ~ 0 + as.factor(SURV) + as.factor(YEAR) + s(TEMP)
Mesh: mesh_sdm (isotropic covariance)
Time column: YEAR
Data: data
Family: tweedie(link = 'log')
 
Conditional model:
                    coef.est coef.se
as.factor(SURV)CRAB     4.95    0.40
as.factor(SURV)SUM      2.69    0.34
as.factor(YEAR)2020    -0.14    0.43
as.factor(YEAR)2021    -0.19    0.33
as.factor(YEAR)2022    -0.77    0.42
as.factor(YEAR)2023    -0.62    0.33
as.factor(YEAR)2024    -0.91    0.34
sTEMP                   0.80    0.83

Smooth terms:
          Std. Dev.
sds(TEMP)      3.15

Dispersion parameter: 23.42
Tweedie p: 1.40
Matern range: 55.04
Spatial SD: 1.12
Spatiotemporal IID SD: 0.96
ML criterion at convergence: 5912.795

See ?tidy.sdmTMB to extract these values as a data frame.
> AIC(mt)  # Критерий Акаике
[1] 11853.59
> sanity(mt)  # Проверка корректности модели
v Non-linear minimizer suggests successful convergence
v Hessian matrix is positive definite
v No extreme or very small eigenvalues detected
v No gradients with respect to fixed effects are >= 0.001
v No fixed-effect standard errors are NA
v No standard errors look unreasonably large
v No sigma parameters are < 0.01
v No sigma parameters are > 100
v Range parameter doesn't look unreasonably large
> 
> mdist <- sdmTMB(
+   data = data, 
+   formula = Density ~ 0+ as.factor(SURV) + as.factor(YEAR)+s(DIST),  # Формула: плотность зависит от года
+   time = "YEAR",         # Временная переменная
+   mesh = mesh_sdm,       # Пространственная сетка
+   family = tweedie(link = "log"),  # Статистическое распределение
+   spatial = "on",        # Включение пространственных эффектов
+   spatiotemporal = "iid" # Пространственно-временные эффекты
+ )
> 
> 
> # Вывод результатов модели
> summary(mdist)
Spatiotemporal model fit by ML ['sdmTMB']
Formula: Density ~ 0 + as.factor(SURV) + as.factor(YEAR) + s(DIST)
Mesh: mesh_sdm (isotropic covariance)
Time column: YEAR
Data: data
Family: tweedie(link = 'log')
 
Conditional model:
                    coef.est coef.se
as.factor(SURV)CRAB     4.74    0.44
as.factor(SURV)SUM      2.55    0.37
as.factor(YEAR)2020    -0.57    0.36
as.factor(YEAR)2021    -0.20    0.36
as.factor(YEAR)2022    -0.61    0.36
as.factor(YEAR)2023    -0.60    0.36
as.factor(YEAR)2024    -0.85    0.36
sDIST                  -0.06    0.16

Smooth terms:
          Std. Dev.
sds(DIST)         0

Dispersion parameter: 23.11
Tweedie p: 1.41
Matern range: 63.83
Spatial SD: 1.22
Spatiotemporal IID SD: 0.97
ML criterion at convergence: 5914.594

See ?tidy.sdmTMB to extract these values as a data frame.

**Possible issues detected! Check output of sanity().**
> AIC(mdist)  # Критерий Акаике
[1] 11857.19
> sanity(mdist)  # Проверка корректности модели
v Non-linear minimizer suggests successful convergence
v Hessian matrix is positive definite
v No extreme or very small eigenvalues detected
v No gradients with respect to fixed effects are >= 0.001
v No fixed-effect standard errors are NA
x `ln_smooth_sigma` standard error may be large
i Try simplifying the model, adjusting the mesh, or adding priors

v No sigma parameters are < 0.01
v No sigma parameters are > 100
v Range parameter doesn't look unreasonably large
> 

5.3.0.1 1. Базовая модель (SURV + YEAR)

Density ~ 0 + as.factor(SURV) + as.factor(YEAR)

• AIC: 11853.31

• Проверка стабильности: Все параметры стабильны

• Ключевые эффекты:

  • Высокая плотность в съемках CRAB (коэф. 4.75)

  • Снижение плотности во всех годах относительно базового уровня (2020-2024: -0.57 до -0.85)

• Пространственные параметры:

  • Диапазон Матерна: 63.53 км

  • Пространственная SD: 1.22

5.3.0.2 2. Модель с глубиной (DEPTH)

Density ~ 0 + as.factor(SURV) + as.factor(YEAR) + s(DEPTH)

• AIC: 11842.73 (наилучший)

• Проверка стабильности: Все параметры стабильны

• Ключевые эффекты:

  • Сильное отрицательное влияние глубины (коэф. -0.60, SE=0.42)

  • Усиление контраста между съемками CRAB/SUM (CRAB: 5.42 vs SUM: 3.09)

• Улучшения:

  • Снижение AIC на 10.58 пунктов

  • Уменьшение пространственного диапазона (40.20 км)

• Интерпретация: Глубина — значимый экологический фактор распределения

5.3.0.3 3. Модель с температурой (TEMP)

Density ~ 0 + as.factor(SURV) + as.factor(YEAR) + s(TEMP)

• AIC: 11853.59 (хуже базовой)

• Проверка стабильности: Стабильна, но высокий SE сглаживания

• Ключевые эффекты:

  • Слабый положительный эффект температуры (коэф. 0.80, SE=0.83)

  • Незначительное изменение годовых эффектов

• Проблемы: Минимальное улучшение модели, высокая неопределенность эффекта температуры

5.3.0.4 4. Модель с расстоянием (DIST)

Density ~ 0 + as.factor(SURV) + as.factor(YEAR) + s(DIST)

• AIC: 11857.19 (наихудший)

• Проверка стабильности: Проблемы со сглаживанием

• Ключевые эффекты:

  • Незначительный эффект расстояния (коэф. -0.06, SE=0.16)

  • Практически идентична базовой модели

• Проблемы: Наихудший AIC, предупреждения о нестабильности

5.3.1 Сводка сравнения моделей

Модель	AIC	ΔAIC	Стабильность	Ключевой предиктор	Эффект ковариаты
DEPTH	11842.73	-	✓✓✓	Глубина	Сильный (-0.60)
Базовая	11853.31	+10.6	✓✓✓	-	-
TEMP	11853.59	+10.9	✓✓	Температура	Слабый (+0.80)
DIST	11857.19	+14.5	✗	Расстояние	Незначительный (-0.06)

5.3.2 Рекомендации

1. Лучшая модель: С глубиной (DEPTH)

   • Значительное улучшение AIC (-10.58)

   • Биологически интерпретируемый эффект (глубина — ключевой фактор распределения краба)

   • Стабильные оценки параметров

2. Практическое значение:

   • Глубина объясняет ~12% пространственной вариабельности (судя по изменению пространственной SD)

   • Модель адекватно отражает экологические предпочтения вида

Вывод: Включение глубины как ковариаты существенно улучшает модель, тогда как температура и расстояние не дают значимых улучшений.

5.4 Визуализация эффектов

Модель с глубиной - md (см. передыдущий скрипт)

# ---------------------------------------------------
# 8.1. ВИЗУАЛИЗАЦИЯ ЭФФЕКТА ГЛУБИНЫ
# ---------------------------------------------------

# Создаем новый датафрейм для предсказаний
newdata <- expand.grid(
  DEPTH = seq(50, 400, by = 2),
  YEAR = 2020,
  SURV = "CRAB",
  xkm = mean(data$xkm),
  ykm = mean(data$ykm)
)

# Делаем предсказания с расчетом стандартных ошибок
pred <- predict(md, newdata = newdata, re_formula = NA, se_fit = TRUE)


# Визуализируем эффект глубины
ggplot(pred, aes(x = DEPTH, y = exp(est))) +
  geom_line(linewidth = 1.2, color = "blue4") +
  geom_ribbon(
    aes(
      ymin = exp(est - 1.96 * est_se), 
      ymax = exp(est + 1.96 * est_se)  # Исправлено на se.fit
    ),
    alpha = 0.3, 
    fill = "steelblue"
  ) +
  labs(
    title = "Эффект глубины на плотность краба",
    subtitle = "Год: 2020, Тип съемки: CRAB",
    x = "Глубина (м)",
    y = "Предсказанная плотность (особей/км²)"
  ) +
  theme_bw(base_size = 14) +
  theme(panel.grid.minor = element_blank())

Рис. 9.: Визуализация эффекта глубины на плотность краба

5.5 Карта с акцентом на нулевые уловы

Повторяем базовую оценку, но меняем в карте нулевые уловы на крестики

Рис. 10.: Визуализация результатов (КАРТА)

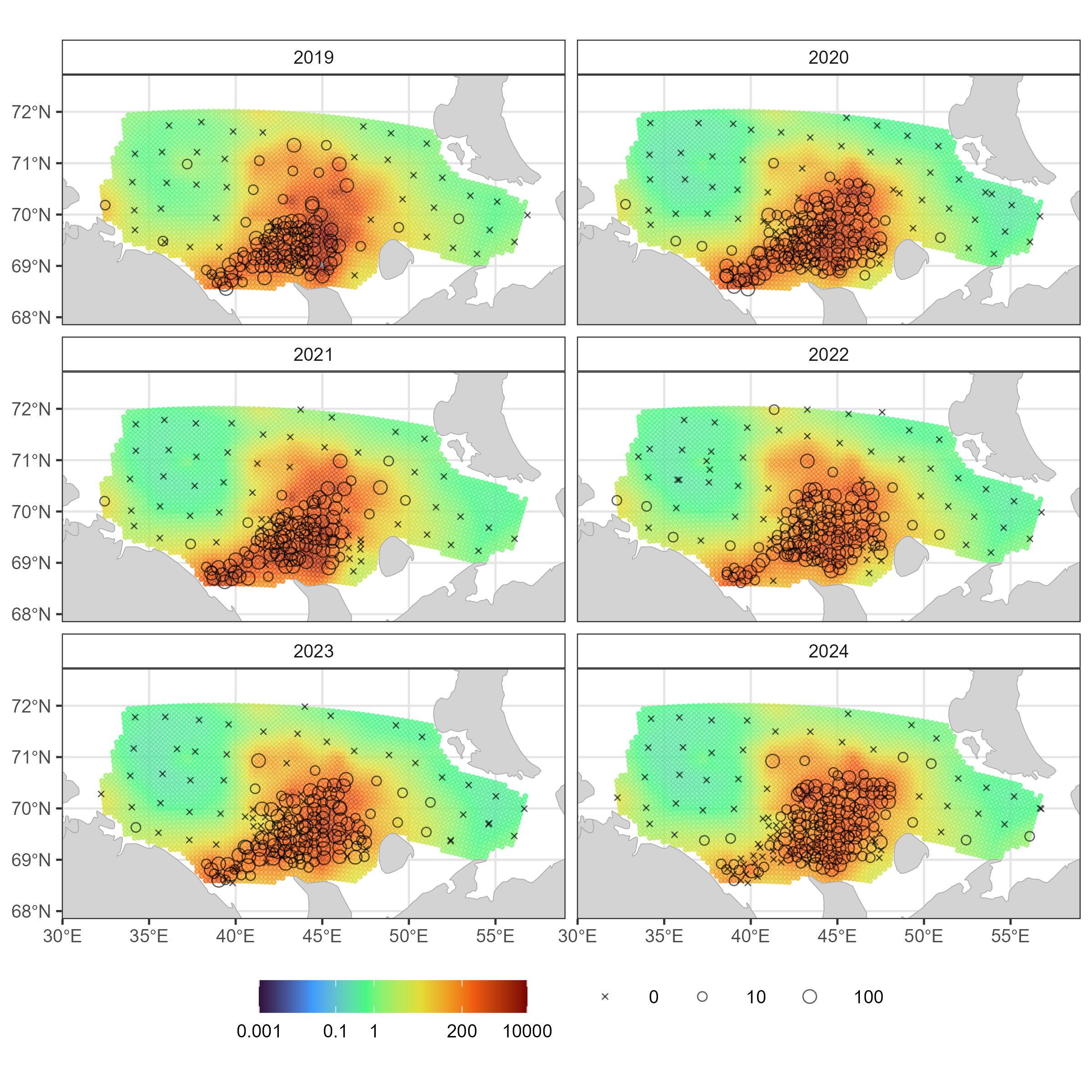
Скрипт для карты с базовой оценкой

# ---------------------------
# 1. ПОДГОТОВКА СРЕДЫ И ДАННЫХ
# ---------------------------

# Очистка рабочей среды
rm(list = ls())

# Установка рабочей директории (замените на свою)
setwd("C:/COMBINE/")

# Загрузка необходимых пакетов
library(readxl)       # Для чтения Excel-файлов
library(ggplot2)      # Визуализация данных
library(dplyr)        # Обработка данных
library(PBSmapping)   # Для работы с пространственными данными
library(sdmTMB)       # Пространственно-временное моделирование
library(INLA)         # Продвинутые пространственные модели
library(sp)           # Классы для пространственных данных
library(sf)           # Пространственные данные (современный формат)
library(rnaturalearth) # Загрузка картографических данных

# Загрузка данных из Excel-файла
data <- readxl::read_excel("KARTOGRAPHIC.xlsx", sheet = "SURVEY")

# Просмотр структуры данных
str(data)


# --------------------------------------------------
# 2. ПРЕОБРАЗОВАНИЕ КООРДИНАТ В ПРОЕКЦИЮ UTM (в км)
# --------------------------------------------------

# Создание пространственного объекта из данных
data_sf <- st_as_sf(
  data, 
  coords = c("X", "Y"), # Указание столбцов с координатами
  crs = 4326            # Система координат WGS84 (широта/долгота)
) 

# Преобразование в UTM зону 37N (метры)
data_utm <- st_transform(data_sf, crs = 32637) 

# Извлечение координат и перевод в километры
utm_coords <- st_coordinates(data_utm)
data$xkm <- utm_coords[, 1] / 1000  # X в км
data$ykm <- utm_coords[, 2] / 1000  # Y в км

# Очистка временных объектов
rm(data_sf, data_utm, utm_coords)

# -----------------------------------------
# 3. ОПРЕДЕЛЕНИЕ ГРАНИЦ ИССЛЕДОВАНИЯ
# -----------------------------------------

# Вычисление границ исследовательского полигона
xl <- c(min(data$xkm), max(data$xkm))  # Границы по X
yl <- c(min(data$ykm), max(data$ykm))  # Границы по Y

# ----------------------------------------
# 4. СОЗДАНИЕ РАСТРОВОЙ СЕТКИ ДЛЯ МОДЕЛИ
# ----------------------------------------

# Создание равномерной сетки с шагом 10 км (для визуализации карты использовался шаг 2 км
GRID <- makeGrid(
  x = seq(xl[1], xl[2], 10), 
  y = seq(yl[1], yl[2], 10),
  byrow = FALSE,
  projection = "UTM", 
  zone = 37
)

# Расчет центроидов ячеек сетки
GRID <- calcCentroid(GRID, rollup = 3)

# -----------------------------------------------------------
# 5. ПОСТРОЕНИЕ ВЫПУКЛОЙ ОБОЛОЧКИ (CONVEX HULL) ДЛЯ ДАННЫХ
# -----------------------------------------------------------

# Создание выпуклой оболочки вокруг точек данных
Hull <- inla.nonconvex.hull(cbind(data$xkm, data$ykm), convex = -0.03)

# Визуализация оболочки 
 plot(Hull)

# Визуализация оболочки и точек съемок 2019-2024
points(data$xkm, data$ykm, pch=1, cex=0.55,col="black")


# Фильтрация сетки: оставляем только точки внутри оболочки
line <- Hull$loc[, 1:2] %>% as.data.frame()
colnames(line) <- c("X", "Y")
GRID$AREA <- point.in.polygon(GRID$X, GRID$Y, line$X, line$Y)
GRID <- GRID[GRID$AREA > 0.1, c("X", "Y")]  # Только внутренние точки

# -------------------------------------------------
# 6. ПОДГОТОВКА СЕТКИ ДЛЯ ПРОГНОЗИРОВАНИЯ
# -------------------------------------------------

# Создание временной сетки (для каждого года)
grid <- replicate_df(GRID, "YEAR", unique(data$YEAR))
colnames(grid) <- c("xkm", "ykm", "YEAR")
grid$SURV <- "CRAB"  # Добавляем информацию о типе съемки

# Визуализация оболочки и сетки для прогнозирования (grid}
 plot(Hull)
 points(grid$xkm, grid$ykm, pch=1, cex=0.55,col="black")

# ---------------------------------------------------
# 7. ПОСТРОЕНИЕ ПРОСТРАНСТВЕННОЙ СЕТКИ (MESH)
# ---------------------------------------------------

# Создание треугольной сетки для пространственного моделирования
mesh_sdm <- make_mesh(
  data, 
  c("xkm", "ykm"),  # Координаты
  cutoff = 10        # Минимальное расстояние между узлами (км)
)

# Визуализация сетки (раскомментируйте)
 plot(mesh_sdm)

# ---------------------------------------------------
# 8. ПОСТРОЕНИЕ ПРОСТРАНСТВЕННО-ВРЕМЕННОЙ МОДЕЛИ
# ---------------------------------------------------

m <- sdmTMB(
  data = data, 
  formula = Density ~ 0 + as.factor(YEAR),  # Формула: плотность зависит от года
  time = "YEAR",         # Временная переменная
  mesh = mesh_sdm,       # Пространственная сетка
  family = tweedie(link = "log"),  # Статистическое распределение
  spatial = "on",        # Включение пространственных эффектов
  spatiotemporal = "iid" # Пространственно-временные эффекты
)


# Вывод результатов модели
summary(m)
AIC(m)  # Критерий Акаике
sanity(m)  # Проверка корректности модели

# ---------------------------------------------------
# 9. ДИАГНОСТИКА МОДЕЛИ
# ---------------------------------------------------

# Расчет остатков модели
data$resids <- residuals(m) 

# Гистограмма остатков
hist(data$resids)

# График квантиль-квантиль
qqnorm(data$resids)
abline(a = 0, b = 1)

# ---------------------------------------------------
# 10. ПРОГНОЗИРОВАНИЕ НА СЕТКЕ
# ---------------------------------------------------

# Прогноз значений плотности на сетке
predictions <- predict(m, newdata = grid, return_tmb_object = TRUE)
RASP <- predictions$data

# Преобразование координат обратно в широту/долготу
RASP$xkm_m <- RASP$xkm * 1000  # Обратно в метры
RASP$ykm_m <- RASP$ykm * 1000

# Создание пространственного объекта в UTM
utm_proj <- CRS("+proj=utm +zone=37 +datum=WGS84 +units=m +no_defs")
coords <- cbind(RASP$xkm_m, RASP$ykm_m)
sp_points <- SpatialPoints(coords, proj4string = utm_proj)

# Преобразование в WGS84 (широта/долгота)
wgs84_proj <- CRS("+proj=longlat +datum=WGS84")
sp_points_latlon <- spTransform(sp_points, wgs84_proj)

# Добавление координат в основной датафрейм
RASP$X <- coordinates(sp_points_latlon)[, 1]  # Долгота
RASP$Y <- coordinates(sp_points_latlon)[, 2]  # Широта

# Удаление временных столбцов
RASP$xkm_m <- NULL
RASP$ykm_m <- NULL

# Проверка структуры результата
str(RASP)

# ---------------------------------------------
# 11. ВИЗУАЛИЗАЦИЯ РЕЗУЛЬТАТОВ (КАРТА)
# ---------------------------------------------

# Загрузка картографических данных
world <- ne_countries(scale = "medium", returnclass = "sf")

# Определение региона интереса (Арктика России)
arctic_bbox <- st_bbox(c(xmin = 25, xmax = 70, ymin = 65, ymax = 80), crs = 4326)
arctic <- st_crop(world, arctic_bbox)

# Определяем кастомные breaks для шкалы
my_breaks <- c(0.001,0.1,1,  200, 10000)

# Создаем категории для PROM
data <- data %>%
  mutate(
    PROM_cat = case_when(
      PROM == 0 ~ "0",
      PROM >= 1 & PROM < 10 ~ "1-9",
      PROM >= 10 & PROM < 100 ~ "10-99",
      PROM >= 100 ~ "100+"
    ),
    PROM_cat = factor(PROM_cat, levels = c("0", "1-9", "10-99", "100+")),
    shape_cat = ifelse(PROM_cat == "0", "zero", "non_zero")
  )

# Обновляем график
ggplot() +
  geom_point(
    data = RASP, 
    aes(x = X, y = Y, color = exp(est)), 
    size = 0.8, 
    alpha = 0.7
  ) + 
  geom_point(
    data = data, 
    aes(x = X, y = Y, size = PROM_cat, shape = shape_cat),
    color = "black", 
    fill = NA, 
    alpha = 0.6
  ) +
  scale_size_manual(
    name = NULL,
    values = c("0" = 1, "1-9" = 2, "10-99" = 3),
    labels = c("0", "10", "100")
  ) +
  scale_shape_manual(
    values = c("zero" = 4, "non_zero" = 21),
    guide = "none" # Скрываем легенду для формы
  ) +
  guides(
    size = guide_legend(
      override.aes = list(shape = c(4, 21, 21)) # Крестик только для первого элемента
    )
  ) +
  geom_sf(data = arctic, fill = "lightgrey", color = "darkgrey") +
  scale_color_viridis_c(
    name = NULL,
    option = "H", 
    trans = "log", 
    breaks = my_breaks, 
    labels = my_breaks, 
    limits = range(my_breaks),
    guide = guide_colorbar(
      barwidth = unit(5, "cm"),
      title.position = "top",
      direction = "horizontal"
    )
  ) +
  facet_wrap(~ YEAR, ncol = 2) +
  coord_sf(
    xlim = c(min(RASP$X)-1, max(RASP$X)+1),
    ylim = c(min(RASP$Y)-0.5, max(RASP$Y)+0.5),
    crs = 4326
  ) +
  theme_bw(base_size = 12) +
  labs(x = NULL, y = NULL) +
  theme(
    panel.grid = element_line(color = "grey90"),
    legend.position = "bottom",
    legend.key.width = unit(1.2, "cm"),
    strip.background = element_rect(fill = "white")
  )


# Сохранение графика (раскомментируйте)
# ggsave("sdmTMBmapZero.jpg", width = 8, height = 8, dpi = 300)

5.6 Определение площади съемки

# ---------------------------
# 1. ПОДГОТОВКА СРЕДЫ И ДАННЫХ
# ---------------------------

# Очистка рабочей среды
rm(list = ls())

# Установка рабочей директории (замените на свою)
setwd("C:/COMBINE/")

# Загрузка необходимых пакетов
library(readxl)       # Для чтения Excel-файлов
library(PBSmapping)   # Для работы с пространственными данными
library(sdmTMB)       # Пространственно-временное моделирование
library(INLA)         # Продвинутые пространственные модели

# Загрузка данных из Excel-файла
data <- readxl::read_excel("KARTOGRAPHIC.xlsx", sheet = "SURVEY")

# Просмотр структуры данных
str(data)


# --------------------------------------------------
# 2. ПРЕОБРАЗОВАНИЕ КООРДИНАТ В ПРОЕКЦИЮ UTM (в км)
# --------------------------------------------------

# Создание пространственного объекта из данных
data_sf <- st_as_sf(
  data, 
  coords = c("X", "Y"), # Указание столбцов с координатами
  crs = 4326            # Система координат WGS84 (широта/долгота)
) 

# Преобразование в UTM зону 37N (метры)
data_utm <- st_transform(data_sf, crs = 32637) 

# Извлечение координат и перевод в километры
utm_coords <- st_coordinates(data_utm)
data$xkm <- utm_coords[, 1] / 1000  # X в км
data$ykm <- utm_coords[, 2] / 1000  # Y в км

# Очистка временных объектов
rm(data_sf, data_utm, utm_coords)

# -----------------------------------------
# 3. ОПРЕДЕЛЕНИЕ ГРАНИЦ ИССЛЕДОВАНИЯ
# -----------------------------------------

# Вычисление границ исследовательского полигона
xl <- c(min(data$xkm), max(data$xkm))  # Границы по X
yl <- c(min(data$ykm), max(data$ykm))  # Границы по Y

# ----------------------------------------
# 4. СОЗДАНИЕ РАСТРОВОЙ СЕТКИ ДЛЯ МОДЕЛИ
# ----------------------------------------

# Создание равномерной сетки с шагом 10 км (для визуализации карты использовался шаг 2 км
GRID <- makeGrid(
  x = seq(xl[1], xl[2], 10), 
  y = seq(yl[1], yl[2], 10),
  byrow = FALSE,
  projection = "UTM", 
  zone = 37
)

# Расчет центроидов ячеек сетки
GRID <- calcCentroid(GRID, rollup = 3)

# -----------------------------------------------------------
# 5. ПОСТРОЕНИЕ ВЫПУКЛОЙ ОБОЛОЧКИ (CONVEX HULL) ДЛЯ ДАННЫХ
# -----------------------------------------------------------

# Создание выпуклой оболочки вокруг точек данных
Hull <- inla.nonconvex.hull(cbind(data$xkm, data$ykm), convex = -0.03)

# Визуализация оболочки 
 plot(Hull)

# Преобразование Hull в объект PolySet:
polys <- data.frame(
  PID = rep(1, nrow(Hull$loc)), # ID полигона
  POS = 1:nrow(Hull$loc),       # Порядок точек
  X = Hull$loc[, 1],            # Координата X (в км)
  Y = Hull$loc[, 2]             # Координата Y (в км)
)
polys <- PBSmapping::as.PolySet(polys, projection = "UTM", zone = 37)

# Расчет площади:
area <- PBSmapping::calcArea(polys)
print(paste("Площадь Hull:", round(area$area, 2), "км кв."))

[1] “Площадь Hull: 283947.5 км кв.”